

☆
1
Comments:
An iconic paper dealing with autoencoders and layer by layer pretraining of deep neural networks.
Layer by layer pretraining of a deep neural network allows finding a good initialization for the subsequent backprop fine tuning of the hole network.
It nicely concludes "It has been obvious since the 1980s that backpropagation through deep autoencoders would be very effective for nonlinear dimensionality reduction, provided that computers were fast enough, data sets were big enough, and the initial weights were close enough to a good solution. All three conditions are now satisfied.".
### Scales quadratically with the dimensionality of the input?
I read: "autoencoders [...] can be applied to very large data sets because both the pretraining and the fine-tuning scale linearly in time and space with the number of training cases."
Indeed it does scale linearly with the number of training cases. However, I think that the method scales quadratically with the dimensionality of the input data as the two first layers seem to have similar sizes.
Is there any way to adapt the method for very high dimensional data? Indeed, if the input dimensionality is 1M, then the method may not scale as it will require a number of connections in the order of $(1M)^2$.
Is it ok if the second layer is already small compared to the dimensionality of the input data?
Or is it ok if the connections between the first two layers are sparse (not all connections are there, just a linear number of them)?
☆
1
Comments:
Very nice paper!
The main idea: if the distance between two embedded nodes has to be large then one should not waste energy in order to make this distance a bit smaller.
Trying to make large distances a bit smaller is actually what Laplacian embedding is doing with its quadratic objective.
One should rather focus on small distances and give up on the pairs of embedded nodes that are far away.
### Embedding complex networks:
This method could be applied to social networks (or complex networks in general): social networks are known to have "weak ties" (roughly speaking, weak ties are links between people that do not have many friends in common) that may perturb laplacian embedding.
### Asymptotic complexity and scalability in practice:
The suggested algorithm to solve the optimization does not seem very scalable. The asymptotic running time complexity is not given.
### Concerns about the optimization in dimension higher than 1. The example in 2-D.
In equations (9-11), what if we change the constraints into: $||x||^2+||y||^2=1$, $e^Tx=0$ and $e^Ty=0$?
In n-D, denoting $r_i$ the vector associated to node $i$, that would give $\sum_ir_i^2=1$ and $\sum_ir_i=0$.
This seems to be a more relevant optimization to me: minimize the distance between nodes in 2-D without setting constraints for each dimension, but rather global constraints.
If the objective is the one of the laplacian embedding, is it true that, in the optimal solution, $y$ will be proportional to $x$? ($x$ and $y$ will both be proportional to the eigenvector associated with the smallest eigenvalue of the Laplacian?)
If so, is it still true if the objective is another one? Like the Cauchy embedding objective for instance?
### Others:
- How to tune the parameter $\sigma$?
> - How to tune the parameter $σ$?
I don't see where $σ$ is defined, did I miss something?
Note that $\sum_i r_i = 0$ means that vector $r$ is orthogonal to
vector $v_0 = (1,1,\ldots\,1,1,1)$. The latter corresponds to the
smallest eigen-value $\lambda_0 = 0$ of [Laplacian
matrix](https://en.wikipedia.org/wiki/Laplacian_matrix). Adding
constraint $r \perp v_0$ to the optimization problem drives us to seek
the second smallest eigenpair.
You may also read very related and well-written
[lecture](https://ocw.mit.edu/courses/mathematics/18-409-topics-in-theoretical-computer-science-an-algorithmists-toolkit-fall-2009/lecture-notes/MIT18_409F09_scribe3.pdf)
about Rayleigh quotients, min-max theorem (Courant–Fischer–Wey). Gives
a good background in the field of eigen-based solutions for
optimization problems.
In 2016, during the preparation of [my
talk](http://www.complexnetworks.fr/temporal-density-of-complex-networks-and-ego-community-dynamics/)
titled "Temporal density of complex networks and ego-community
dynamics"
([slides](https://kirgizov.link/talks/temporal-density-4-july-2016.pdf),
french). I have read stuff about graph optimization problems. Below I
present my personal (perhaps a little bit random selection) of related
papers and books
* [Four Cheeger-type Inequalities for Graph Partitioning Algorithms](https://www.math.ucsd.edu/~fan/wp/heaticcm.pdf), Fan Chung, 2007
* [Normalized cuts and image segmentation](https://people.eecs.berkeley.edu/~malik/papers/SM-ncut.pdf), Jianbo Shi and Jitendra Malik, 2000
* [Eigenvalues of graphs](https://web.cs.elte.hu/~lovasz/eigenvals-x.pdf), László Lovász, 2007
* [Spectres de graphes](https://www-fourier.ujf-grenoble.fr/~ycolver/All-Articles/98a.pdf) de Yves Colin de Verdière, 1998




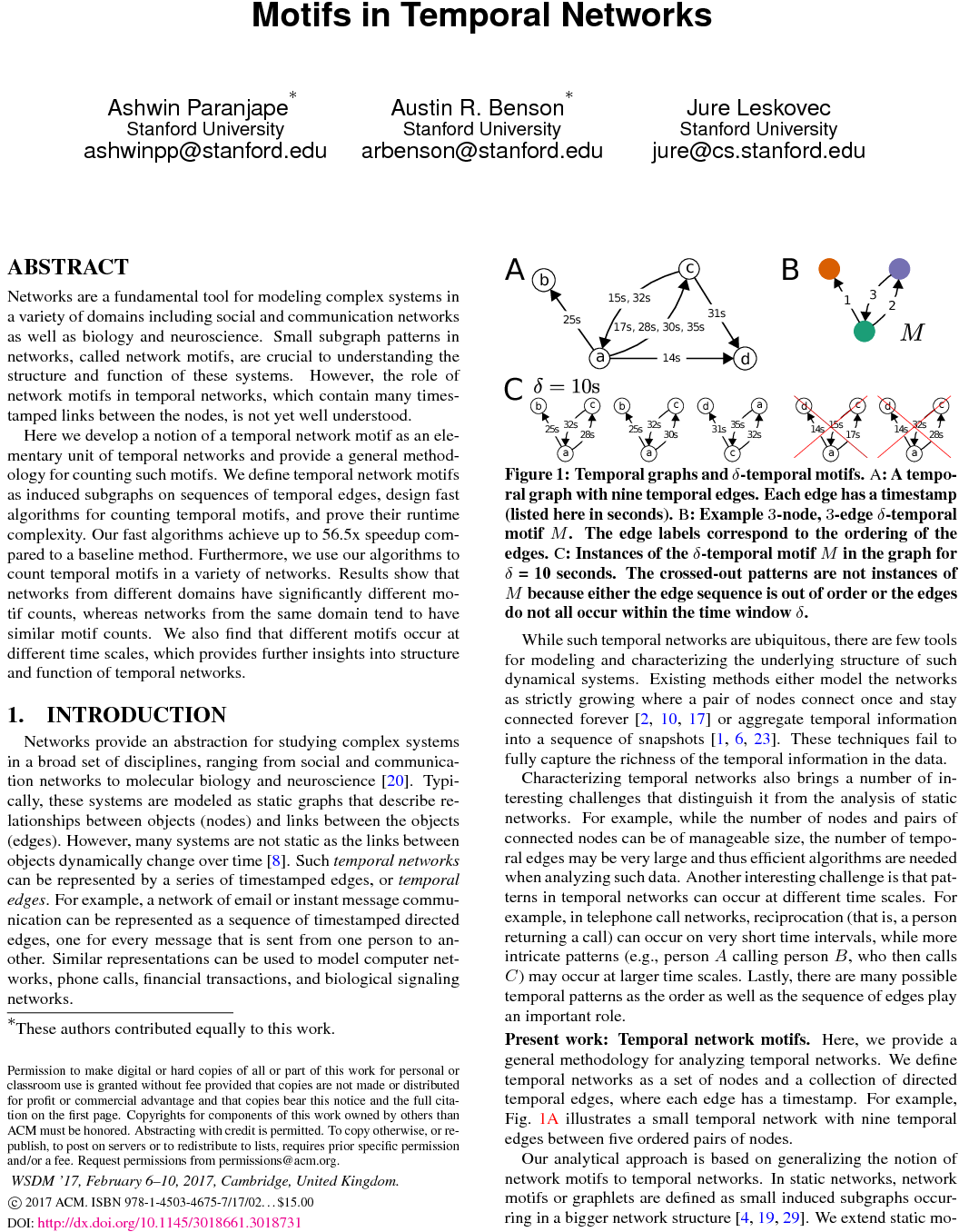
Comments: