Papers^γ

Some algorithms: * [Efficient computation of absent words in genomic sequences](https://pubmed.ncbi.nlm.nih.gov/18366790) paper by Julia Herold, Stefan Kurtz and Robert Giegerich. * [keeSeek algo](http://www.medcomp.medicina.unipd.it/main_site/doku.php?id=keeseek) from [keeSeek: searching distant non-existing words in genomes for PCR-based applications](https://academic.oup.com/bioinformatics/article/30/18/2662/2475409) paper by Marco Falda, Paolo Fontana, Luisa Barzon, Stefano Toppo and Enrico Lavezzo. Can these algorithms be improved ?

Great paper! A pleasure to read! - Using the proposed ordering divides the running time by no more than two compared to using other orderings. This is a bit disappointing. - Why no comparison against a random permutation of the nodes? I'm curious how bad a random ordering performs. - "the optimal score $F_w$ cannot be computed due to the NP-hard complexity": such as it is, this statement is not true since only a few real-world datasets are considered. In practice, these real-world datasets could lead to easy instances of the problem. - Is there any publicly available implementation of the proposed algorithm? I find the following paragraph confusing: "In general, the problem of finding the optimal graph ordering by maximizing $F(\phi)$ is the problem of solving maxTSP-$w$ with a window size $w$ as a variant of the maxTSP problem. To solve the graph ordering problem as maxTSP-$w$, we can construct an edge-weighted complete undirected graph $G_w$ from $G$. Here, $V(G_w) =V(G)$, and there is an edge $(v_i, v_j)\in E(G_w)$ for any pair of nodes in $V(G_w)$. The edge-weight for an edge (vi, vj) in $G_w$, denoted as $s_{ij}$, is $S(v_i, v_j)$ computed for the two nodes in the original graph $G$. Then the optimal maxTSP-$w$ over $G$ is the solution of maxTSP over $G$. Note that maxTSP only cares the weight between two adjacent nodes, whereas maxTSP-$w$ cares the sum of weights within a window of size $w$." I think that: - The index $w$ of $G_w$ does not refer to the window size $w$, but stands for "weight". - It should be "the optimal $F(\Phi)$ over $G$ is the solution of maxTSP-$w$ over $G_w$" instead of "the optimal maxTSP-$w$ over $G$ is the solution of maxTSP over $G$". - On the same line, in the paragraph above that one: "The optimal graph ordering, for the window size $w= 1$, by maximizing $F(\Phi)$ is equivalent to the maximum traveling sales-man problem, denoted as maxTSP for short.". It should be clear that maxTSP should be solve on $G_w$, where $w$ stands for weight: complete graph with weight $S(u,v)$ on the edge $u,v$. MINORS: - "The night graph algorithms" and "the night orderings": "night" instead of "nine".

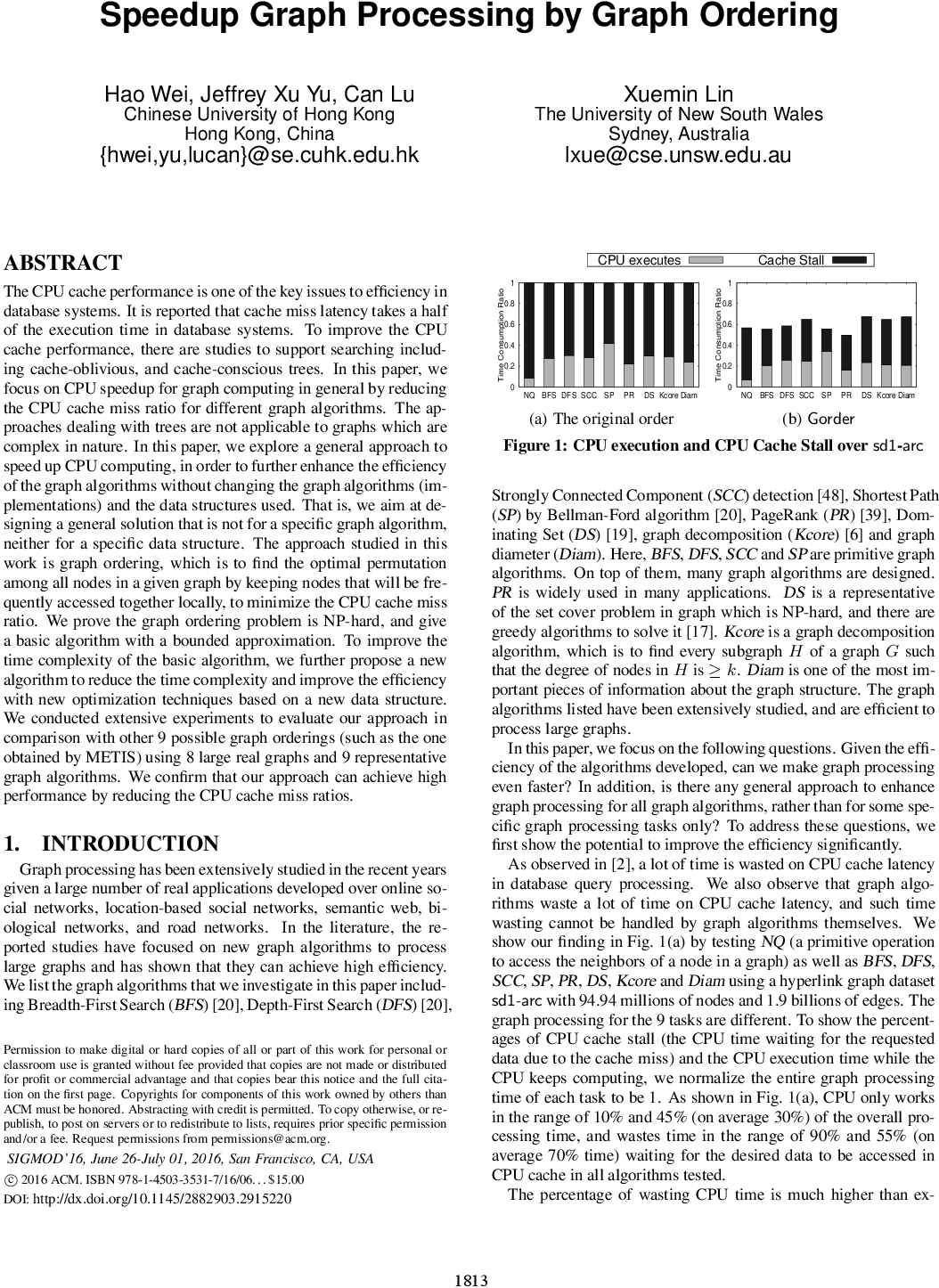
Interesting comments. > - Using the proposed ordering divides the running time by no more than two compared to using other orderings. This is a bit disappointing. Yes, but from Figure 1, we can draw that we cannot expect much more than this... Maybe 3 or 4 at most. > - "the optimal score $F_w$ cannot be computed due to the NP-hard complexity": such as it is, this statement is not true since only a few real-world datasets are considered. In practice, these real-world datasets could lead to easy instances of the problem. Very relevant, still it looks very much like looking for the best solution of a TSPw on a real instance. I understand that they actually found the optimal $ F_w $ in some cases (Table 1).

Every time I see how people optimize CPU or disk cache usage, I admire it. It makes me think that optimizing the [speculative execution](https://en.wikipedia.org/wiki/Speculative_execution) and branch prediction could also be used to this end.

A famous example of the periodicity forcing word equation is $xy = yx$. It means that if a word $xy$ equals to a word $yx$, obtained by a _cut-and-swap_ process, there exists a word $w$ and integers $i,j$ such that $x = w^i$ and $y = w^j$. The paper's Section 1 and 5 contain a brief yet very helpful overview of existing results about periodicity forcing. About ten years ago, Czeizler, Kari and Seki, in their work [On a special class of primitive words](https://www.csd.uwo.ca/~lkari/mfcs.pdf), have introduced a notion of a pseudo-repetition. It can be explained with the following example. When DNA molecules are regarded as words, the Watson-Crick correspondence $$G \sim C, A \sim T$$ between guanine ($G$) and cytosine ($C$), adenine ($A$) and thymine ($T$) allows us to say that a word $ATCGATTGAGCTCTAGCG$ contains the same information as the word $TAGCTAACTCGAGATCGC$. A pseudo-repetition is a repetition of a word or its Watson-Crick complement. So, for instance $ATC \sim TAG$, and the word $ATCTAGATCATCTAG$ is a pseudo-repetition of the word $ATC$. In an abstract algebraic setting (involving monoids, morphic permutations, equivalence classes and anticongruences), the author studies an extension to the notion of periodicity forcing, using the recently introduced concept of pseudo-repetitions and related ideas. Holub proves, for instance, that any periodicity forcing classical word equation also forces a pseudo-periodicity. He provides interesting new results and generalizations of already known results. MathSciNet:MR4074724.

Nice coarse-gaining based heuristic to partition the nodes into k sets of similar sizes minimizing the number of edges between those sets. Random maximal matchings are used to coarse-grain the graph. Maybe fast heuristics to obtain a large maximal matching can be considered, such as using the two rules detailed here: [Karp-Sipser based kernels for bipartite graph matching](https://papers-gamma.link/paper/160). Publicly available implementation: http://glaros.dtc.umn.edu/gkhome/metis/metis/overview